Do you have a specific table where you sit down to everyday at lunch? Are the people who eat lunch with you the same group of friends each day? Sometimes, do you sit next to one friend and then maybe, the next day, because you were late getting your lunch, you sit next to someone else but since you're all friends, it really doesn't matter, right?

The Commutative Property is kind of like that. It deals with moving around or 'commuting' and if you look at the root word in commutative and you can remember that the Commuter Lane on the freeway is only for those people who have two or more people in a car, then you can remember this property.

With the Commutative Property you are dealing with changing the order of your group members. So, let's take a look at it with some pictures.

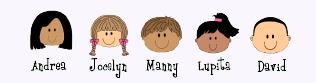Andrea, Jocelyn, Manny, Lupita, and David always eat lunch together. They sit at the same table every single day.

On Monday, they were sitting on the bench in this order.

On Tuesday, David and Andrea wanted to discuss their history test. Manny had stopped at the library before heading to lunch. Their bench order had changed.

This is an example of the Commutative Property where the order changed because the students had moved around.

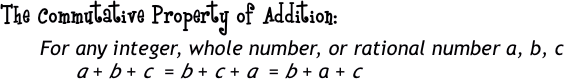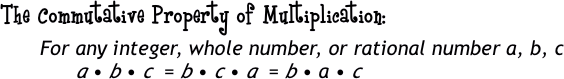Now, let's go back to your group of friends. You probably hang out or associate with the same people most every day right? But, sometimes, even in your group, you may form smaller groups to do stuff or to discuss things or whatever. This is where the Associative Property comes in.

The Associative Property is the grouping property. It is dealing with how terms (or in our example, your friends/group members) are grouped The way that you know that the Associate Property is being used is easy: SYMBOLS like parenthesis, brackets, and braces are used.

The friends all carpool to school and their parents take turns with the carpool duty.

On Mondays, Lupita's mom picks up David and Andrea.

Jocelyn's dad picks up Manny.

For modified days, Lupita's sister picks up David and Lupita. Andrea, Jocelyn, and Manny stay late those days for choir and Jocelyn's dad takes them home.

The groupings for the carpool are different yet everyone gets to and from school without a problem.

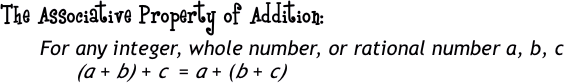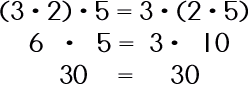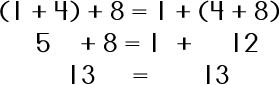You walk into class and there is some strange adult sitting at your teacher's desk. OH NO! Where's my teacher? It's substitute teacher time.

The Substitution Property is just that; if two things are the same, then it doesn't matter if one thing substitutes for the other.

Simplify each of the following expressions by substituting a = 2, b = 5, and c = 9

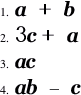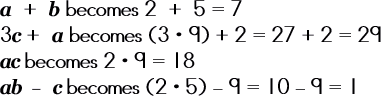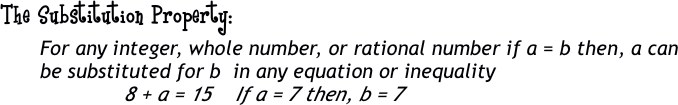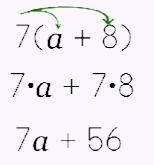
One of the most widely-used properties is the Distributive Property. It is one that SHOULD be learned and memorized because it can help make simplifying expressions and solving equations so much faster! Truly!

The Distributive Property can be thought of as part of the 'G' in GEMA (order of operations) because there's a set of parenthesis involved.

In GEMA, you do whatever is in the grouping symbols (aka, the parenthesis) first, right?

Simplify each of the following using the Distributive Property.

In the order of operations you would normally 'do' whatever is in the parenthesis first. The problem is you cannot combine a variable and a number because these are not like terms.

This is where the Distributive Property comes in.

When you have several terms then it may seem complicated but, it really isn't. It just takes a few more steps to simplify your problem.

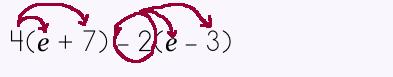Step 1: Take the multiplier across the parenthesis.

Be sure to do EACH 'set' as though they were separate problems because, technically, they are.

Step 2: Do the math. Be careful! Follow through with EACH term.

Step 3: Combine like terms. I recommend doing this in a VERTICAL format (it is so much easier!!).

That's it! Easy-peasy, lemon-squeasy!

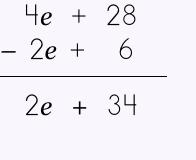©2011–2017 Sherry Skipper Spurgeon. All rights reserved.